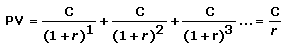Haggis_McMutton wrote:BigBallinStalin wrote:Well, if we jump up the price of each bet, that would increase my opportunity cost. (There's some chance that I could lose an unacceptable amount of money in a very short time).
----> whoops! This isn't betting! I reread the OP....
What price would I pay?
Negative infinity.
(so would homo economicus)
I don't follow, maybe I really suck at explaining this game or something.
Let's do a variation. Let's say we cap it at 2 tosses, if you don't get heads in 2 tosses you don't win anything.
Then the expected value is simple: 1/2 * 2$ + 1/4 * 4$ = 2$.
So if we limit it to 2 tosses homo economicus should be willing to pay 1.99$ to play this game.
The question is what happens if we don't limit it.
I'm being cheeky, but negative infinity is the right answer to your question because that's the
profit-maximizing choice. You would have to pay us an infinite amount of money in order to entice an individual or a homo economicus to play your game.

So to stop me answering with "negative infinity," you have to expand your scenario by placing it into a
competitive environment where more than one person can bid up the price of the game to the point where marginal benefits equal marginal costs (i.e. profit is equal to 0). Assuming perfect information and all those heroic (imaginary) assumptions used by mainstream economists, then the question becomes:
"in a competitive market for this game, what is the most you would be willing to pay?"
I forget my finance classes, but here's an avenue toward the answer:
(1)
find the NPVnet present value = -start-up cost (discussion of rules) - transaction cost (sitting here, flipping a coin, etc.) + (future streams of income/ interest rate)
---> it still goes back to one's time preferences (interest rate and risk), which I'll explain at the end.
---> also, this net present value must then be compared to the opportunity cost (i.e. next highest valued use of one's resources), and the opportunity cost is subjective--it varies across individuals (see: Buchanan's
Cost and Choice), so
there is no one correct answer to this in reality. (a)
Aside from the above problems, how do we calculate the future streams of income from the Haggis' game?It's a
perpetuity.
"A constant stream of identical cash flows with no end. The formula for determining the present value of a perpetuity is as follows":
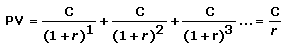
(C would be some amount of revenue multiplied by a probability, and each flip represents some distinct period of time, so each flip gets its own [C/(1+r^n)] value. The interest rate would be scaled down to that extremely small period of time.)
...Although it may seem a bit illogical, an infinite series of cash flows can have a finite present value. Because of the time value of money, each payment is only a fraction of the last.
The concept of a perpetuity is used often in financial theory, such as the dividend discount model (DDM).
In other words, it depends on how one perceives the interest rate at which to discount those streams of income. It's still a subjective matter since interest rate is based on one's
time preference. There is no "right" answer to your question because (1) opportunity costs and (2) interest rates.
If we use the heroic assumptions from mainstream economics, then we may as well argue about angels and pinheads, which is bad economics.