Let's play a game.

[Haggis_McMutton]

Here's the scenario.

We toss a coin. If it comes up heads I give you 2$, if it comes up tails we flip again. If on the second flip it comes up heads I give you 4$, otherwise we flip again and so on.(3rd flip -> 8$, 4th flip -> 16$ etc)

Basically, we keep flipping the coin till it hits heads. If it hits heads on its Nth flip I pay you 2^N dollars.

Question: If you had to pay a fee to play this game, how much would you pay?
How much would a perfectly rational "homo economicus" pay? (if it's different than what you'd pay).

If anyone recognizes this scenario, don't spoil it right away plox.

[rdsrds2120]

I don't recognize it, but it's just a distribution with an expected mean.
Should I not answer since I know how to just plug-n-chug to figure it out?

BMO

[fadedpsychosis]

ok, I'm no statistician... and in fact I was bored to sleep in my statistics class... but I know that I would never play unless the entry fee were ridiculously low (as in equal to or less than 1st flip)... and I know the game would never be played that way. I have horrible luck in anything depending solely on luck, and I'm pretty sure any loss the house might conceivably take from any one person it would make up from me.

[Haggis_McMutton]

I don't recognize it, but it's just a distribution with an expected mean.
Should I not answer since I know how to just plug-n-chug to figure it out?

BMO

I just meant don't link to a page discussing this thing or anything like that.

Feel free to use any rational or occult means at your disposal to arrive at your answer.

ok, I'm no statistician... and in fact I was bored to sleep in my statistics class... but I know that I would never play unless the entry fee were ridiculously low (as in equal to or less than 1st flip)... and I know the game would never be played that way. I have horrible luck in anything depending solely on luck, and I'm pretty sure any loss the house might conceivably take from any one person it would make up from me.

Yeah, it's more of a thought experiment that a real game. Basically the game has some weird properties if you think about it.

[fadedpsychosis]

I don't recognize it, but it's just a distribution with an expected mean.
Should I not answer since I know how to just plug-n-chug to figure it out?

BMO

I just meant don't link to a page discussing this thing or anything like that.

Feel free to use any rational or occult means at your disposal to arrive at your answer.

ok, I'm no statistician... and in fact I was bored to sleep in my statistics class... but I know that I would never play unless the entry fee were ridiculously low (as in equal to or less than 1st flip)... and I know the game would never be played that way. I have horrible luck in anything depending solely on luck, and I'm pretty sure any loss the house might conceivably take from any one person it would make up from me.

Yeah, it's more of a thought experiment that a real game. Basically the game has some weird properties if you think about it.

so the question is "how much would a normal person pay for an exponential growth profit vs exponential decline likelihood"? granting of course that some return is a given in this equation... maybe my brain just doesn't work right for this because I'm not seeing the weirdness... that and you've got me thinking in binary now... thanks for that

[Funkyterrance]

Yeah I know a game where a certain method would simulate this scenario to a degree but I'll be respectful. I should say the amount I would pay to play would depend on my mood/current disposable income. Sounds like a lot of fun though. As far as figuring the statistical analysis of the game I think I would find that decidedly un-fun. I would certainly play for $2 though.
My wheels are definitely turning on this one.

[Frigidus]

It's worth at least $3, considering flipping heads first would give you $2 and flipping tails first would give you at least $4. I'm not sure just how much more than $3 it would be worth though.

[Funkyterrance]

It's worth at least $3, considering flipping heads first would give you $2 and flipping tails first would give you at least $4. I'm not sure just how much more than $3 it would be worth though.

It seems I misread the op. So even if it's tails on the first flip, you get paid?

[BigBallinStalin]

It depends on the opportunity cost. You could have better/more valuable things to do than sitting around flipping a coin for some expected profit (which may result in 0 if done over time = infinity; however, the present discount value of the bet-money depends on one's time preference).

[Haggis_McMutton]

so the question is "how much would a normal person pay for an exponential growth profit vs exponential decline likelihood"? granting of course that some return is a given in this equation...

That's one way of putting it.

How would you evaluate the value of playing this game other than gut feeling (which in your case says it's worth < 2$ I think ? )

maybe my brain just doesn't work right for this because I'm not seeing the weirdness... that and you've got me thinking in binary now... thanks for that

You say that like it's a bad thing.

Yeah I know a game where a certain method would simulate this scenario to a degree but I'll be respectful.

I'm curious what you mean.

It looks like my no spoilers disclaimer is not having the desired effect though. I just meant not to link to a website doing a full analysis of this game. Other than that, feel free to post whatever way of computing the value you may want.

It seems I misread the op. So even if it's tails on the first flip, you get paid?

Looks like I made a typo. I had inverted tails with heads in the third sentence, sorry. Corrected now.

The game is basically flip the coin untill you get the desired outcome, if it took N flips to get this outcome the payout is 2^N.

[Haggis_McMutton]

It depends on the opportunity cost. You could have better/more valuable things to do than sitting around flipping a coin for some expected profit (which may result in 0 if done over time = infinity; however, the present discount value of the bet-money depends on one's time preference).

So, how much would you pay?

What if we multiply the numbers by a random constant so that opportunity cost would be in favour of playing this game (if you can win money at it).
I.E. instead of $2, $4, $8 make it $2000, $4000, $8000 or whatever you want(as long as all payouts are multiplied by the same constant).

[BigBallinStalin]

It depends on the opportunity cost. You could have better/more valuable things to do than sitting around flipping a coin for some expected profit (which may result in 0 if done over time = infinity; however, the present discount value of the bet-money depends on one's time preference).

So, how much would you pay?

What if we multiply the numbers by a random constant so that opportunity cost would be in favour of playing this game (if you can win money at it).
I.E. instead of $2, $4, $8 make it $2000, $4000, $8000 or whatever you want(as long as all payouts are multiplied by the same constant).

Well, if we jump up the price of each bet, that would increase my opportunity cost. (There's some chance that I could lose an unacceptable amount of money in a very short time).

----> whoops! This isn't betting! I reread the OP....


What price would I pay?

Negative infinity.


(so would homo economicus)

[Haggis_McMutton]

Well, if we jump up the price of each bet, that would increase my opportunity cost. (There's some chance that I could lose an unacceptable amount of money in a very short time).

----> whoops! This isn't betting! I reread the OP....


What price would I pay?

Negative infinity.


(so would homo economicus)

I don't follow, maybe I really suck at explaining this game or something.

Let's do a variation. Let's say we cap it at 2 tosses, if you don't get heads in 2 tosses you don't win anything.

Then the expected value is simple: 1/2 * 2$ + 1/4 * 4$ = 2$.

So if we limit it to 2 tosses homo economicus should be willing to pay 1.99$ to play this game.
The question is what happens if we don't limit it.

[Funkyterrance]

Yeah I know a game where a certain method would simulate this scenario to a degree but I'll be respectful.

I'm curious what you mean.

It looks like my no spoilers disclaimer is not having the desired effect though. I just meant not to link to a website doing a full analysis of this game. Other than that, feel free to post whatever way of computing the value you may want.

I was thinking about the tactic at winning roulette by just doubling your bet every time you lose until you eventually have a run of luck that gets you to come out ahead. I know it's not the exact same scenario but there are similarities.

[BigBallinStalin]

Well, if we jump up the price of each bet, that would increase my opportunity cost. (There's some chance that I could lose an unacceptable amount of money in a very short time).

----> whoops! This isn't betting! I reread the OP....


What price would I pay?

Negative infinity.


(so would homo economicus)

I don't follow, maybe I really suck at explaining this game or something.

Let's do a variation. Let's say we cap it at 2 tosses, if you don't get heads in 2 tosses you don't win anything.

Then the expected value is simple: 1/2 * 2$ + 1/4 * 4$ = 2$.

So if we limit it to 2 tosses homo economicus should be willing to pay 1.99$ to play this game.
The question is what happens if we don't limit it.

I'm being cheeky, but negative infinity is the right answer to your question because that's the profit-maximizing choice. You would have to pay us an infinite amount of money in order to entice an individual or a homo economicus to play your game.


So to stop me answering with "negative infinity," you have to expand your scenario by placing it into a competitive environment where more than one person can bid up the price of the game to the point where marginal benefits equal marginal costs (i.e. profit is equal to 0). Assuming perfect information and all those heroic (imaginary) assumptions used by mainstream economists, then the question becomes:

"in a competitive market for this game, what is the most you would be willing to pay?"


I forget my finance classes, but here's an avenue toward the answer:

(1)find the NPV
net present value = -start-up cost (discussion of rules) - transaction cost (sitting here, flipping a coin, etc.) + (future streams of income/ interest rate)
---> it still goes back to one's time preferences (interest rate and risk), which I'll explain at the end.
---> also, this net present value must then be compared to the opportunity cost (i.e. next highest valued use of one's resources), and the opportunity cost is subjective--it varies across individuals (see: Buchanan's Cost and Choice), so there is no one correct answer to this in reality.


(a) Aside from the above problems, how do we calculate the future streams of income from the Haggis' game?

It's a perpetuity.
"A constant stream of identical cash flows with no end. The formula for determining the present value of a perpetuity is as follows":


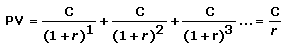
(C would be some amount of revenue multiplied by a probability, and each flip represents some distinct period of time, so each flip gets its own [C/(1+r^n)] value. The interest rate would be scaled down to that extremely small period of time.)

...Although it may seem a bit illogical, an infinite series of cash flows can have a finite present value. Because of the time value of money, each payment is only a fraction of the last.

The concept of a perpetuity is used often in financial theory, such as the dividend discount model (DDM).

In other words, it depends on how one perceives the interest rate at which to discount those streams of income. It's still a subjective matter since interest rate is based on one's time preference. There is no "right" answer to your question because (1) opportunity costs and (2) interest rates.

If we use the heroic assumptions from mainstream economics, then we may as well argue about angels and pinheads, which is bad economics.

[Army of GOD]

I beat you up and steal all of your money

[Haggis_McMutton]

I'm being cheeky, but negative infinity is the right answer to your question because that's the profit-maximizing choice. You would have to pay us an infinite amount of money in order to entice an individual or a homo economicus to play your game.


So to stop me answering with "negative infinity," you have to expand your scenario by placing it into a competitive environment where more than one person can bid up the price of the game to the point where marginal benefits equal marginal costs (i.e. profit is equal to 0). Assuming perfect information and all those heroic (imaginary) assumptions used by mainstream economists, then the question becomes:

"in a competitive market for this game, what is the most you would be willing to pay?"

goddamn economists.

Ok, I guess I should have put the question as:
"The guy running the game charges a fee to play, how low would this fee have to be in order for you to play?".
That should give the same result and avoid the competitive market, I think.

I forget my finance classes, but here's an avenue toward the answer:

(1)find the NPV
net present value = -start-up cost (discussion of rules) - transaction cost (sitting here, flipping a coin, etc.) + (future streams of income/ interest rate)
---> it still goes back to one's time preferences (interest rate and risk), which I'll explain at the end.
---> also, this net present value must then be compared to the opportunity cost (i.e. next highest valued use of one's resources), and the opportunity cost is subjective--it varies across individuals (see: Buchanan's Cost and Choice), so there is no one correct answer to this in reality.


(a) Aside from the above problems, how do we calculate the future streams of income from the Haggis' game?

It's a perpetuity.
"A constant stream of identical cash flows with no end. The formula for determining the present value of a perpetuity is as follows":


(C would be some amount of revenue multiplied by a probability, and each flip represents some distinct period of time, so each flip gets its own [C/(1+r^n)] value. The interest rate would be scaled down to that extremely small period of time.)

...Although it may seem a bit illogical, an infinite series of cash flows can have a finite present value. Because of the time value of money, each payment is only a fraction of the last.

The concept of a perpetuity is used often in financial theory, such as the dividend discount model (DDM).

In other words, it depends on how one perceives the interest rate at which to discount those streams of income. It's still a subjective matter since interest rate is based on one's time preference. There is no "right" answer to your question because (1) opportunity costs and (2) interest rates.

If we use the heroic assumptions from mainstream economics, then we may as well argue about angels and pinheads, which is bad economics.

I think you've got the idea, though the fact I was reffering to as being "weird" about the game seems like it's imbeded in your reasoning rather than spelt out. Maybe you wacky economists don't find it weird.

I don't think it's exactly a perpetuity, since there will be just one payment all in all, but it does seem correct that you should weight the payment by how long it would take you to get it. The larger the potential payment, the more flips it would take you to get it.

I don't want to be too boring about this (hey, if I am you guys will just stop posting in the thread I guess), but just for the purpose of the initial thought experiment, let's make the assumptions that there is no start-up cost (you knew the rules already), and that the whole game is instantaneous, you agree or disagree to play and get the outcome, so there is no transaction or time devaluation involved either and negligible opportunity cost wasted (whatever you could have accomplished in the 5 seconds this whole operation takes).

NOW, how much would you be willing to pay to be allowed to play?

[BigBallinStalin]

I'm being cheeky, but negative infinity is the right answer to your question because that's the profit-maximizing choice. You would have to pay us an infinite amount of money in order to entice an individual or a homo economicus to play your game.


So to stop me answering with "negative infinity," you have to expand your scenario by placing it into a competitive environment where more than one person can bid up the price of the game to the point where marginal benefits equal marginal costs (i.e. profit is equal to 0). Assuming perfect information and all those heroic (imaginary) assumptions used by mainstream economists, then the question becomes:

"in a competitive market for this game, what is the most you would be willing to pay?"

goddamn economists.

Ok, I guess I should have put the question as:
"The guy running the game charges a fee to play, how low would this fee have to be in order for you to play?".
That should give the same result and avoid the competitive market, I think.

$0.000000000000000000000000000000000000000 ... 00000000000000000000000000000000000000000001

I forget my finance classes, but here's an avenue toward the answer:

(1)find the NPV
net present value = -start-up cost (discussion of rules) - transaction cost (sitting here, flipping a coin, etc.) + (future streams of income/ interest rate)
---> it still goes back to one's time preferences (interest rate and risk), which I'll explain at the end.
---> also, this net present value must then be compared to the opportunity cost (i.e. next highest valued use of one's resources), and the opportunity cost is subjective--it varies across individuals (see: Buchanan's Cost and Choice), so there is no one correct answer to this in reality.


(a) Aside from the above problems, how do we calculate the future streams of income from the Haggis' game?

It's a perpetuity.
"A constant stream of identical cash flows with no end. The formula for determining the present value of a perpetuity is as follows":


(C would be some amount of revenue multiplied by a probability, and each flip represents some distinct period of time, so each flip gets its own [C/(1+r^n)] value. The interest rate would be scaled down to that extremely small period of time.)

...Although it may seem a bit illogical, an infinite series of cash flows can have a finite present value. Because of the time value of money, each payment is only a fraction of the last.

The concept of a perpetuity is used often in financial theory, such as the dividend discount model (DDM).

In other words, it depends on how one perceives the interest rate at which to discount those streams of income. It's still a subjective matter since interest rate is based on one's time preference. There is no "right" answer to your question because (1) opportunity costs and (2) interest rates.

If we use the heroic assumptions from mainstream economics, then we may as well argue about angels and pinheads, which is bad economics.

I think you've got the idea, though the fact I was reffering to as being "weird" about the game seems like it's imbeded in your reasoning rather than spelt out. Maybe you wacky economists don't find it weird.

I don't think it's exactly a perpetuity, since there will be just one payment all in all, but it does seem correct that you should weight the payment by how long it would take you to get it. The larger the potential payment, the more flips it would take you to get it.

I don't want to be too boring about this (hey, if I am you guys will just stop posting in the thread I guess), but just for the purpose of the initial thought experiment, let's make the assumptions that there is no start-up cost (you knew the rules already), and that the whole game is instantaneous, you agree or disagree to play and get the outcome, so there is no transaction or time devaluation involved either and negligible opportunity cost wasted (whatever you could have accomplished in the 5 seconds this whole operation takes).

NOW, how much would you be willing to pay to be allowed to play?

How many angels can stand on the head of a pin?

or

$0.000000000000000000000000000000000000000 ... 00000000000000000000000000000000000000000001

[Haggis_McMutton]

$0.000000000000000000000000000000000000000 ... 00000000000000000000000000000000000000000001

He's not offering it for that little. :p

I'll post what I'm reffering to as being weird tommorrow. In case anyone else wants to give their 0.000000000000000000000000000000000000000 ... 00000000000000000000000000000000000000000002 cents in the meantine

[/]

I wouldn't bet on the high stakes one, I don't like high stakes gambles.

I would say 4 dollars would be an enticing number for me to play since I'm not very lucky, Half a chance of losing half the bet, quarter chance of breaking even, quarter chance of winning more. It seems fair enough.

A few questions though
1. Is there any possibility of it being a two headed coin, making me an instant loser?
2. Is there any possibility of it being a two tailed coin, trapping us in some sort of Twilight Zone fate; waiting desperately for the release of death?
3. If so, can I just leave?

[thegreekdog]

Here's the scenario.

We toss a coin. If it comes up heads I give you 2$, if it comes up tails we flip again. If on the second flip it comes up heads I give you 4$, otherwise we flip again and so on.(3rd flip -> 8$, 4th flip -> 16$ etc)

Basically, we keep flipping the coin till it hits heads. If it hits heads on its Nth flip I pay you 2^N dollars.

Question: If you had to pay a fee to play this game, how much would you pay?
How much would a perfectly rational "homo economicus" pay? (if it's different than what you'd pay).

If anyone recognizes this scenario, don't spoil it right away plox.

Do we stop the first time it hits heads? In other words, if it hits heads the first time, would I get my $2 and that would be it?

If yes (which I think is the answer), I would try to pay $1.99 but would pay $2. The person running the game would probably want to charge something more than $2, right? My math sucks.

[john9blue]

Here's the scenario.

We toss a coin. If it comes up heads I give you 2$, if it comes up tails we flip again. If on the second flip it comes up heads I give you 4$, otherwise we flip again and so on.(3rd flip -> 8$, 4th flip -> 16$ etc)

Basically, we keep flipping the coin till it hits heads. If it hits heads on its Nth flip I pay you 2^N dollars.

Question: If you had to pay a fee to play this game, how much would you pay?
How much would a perfectly rational "homo economicus" pay? (if it's different than what you'd pay).

If anyone recognizes this scenario, don't spoil it right away plox.

if i HAD to pay a fee for this game, i would pay one cent, as that is the smallest common non-zero amount of currency which can qualify as a "fee"

[john9blue]

seriously tho...

the average outcome of this game would be:

.5*2 = 1
+.25*4 = 1
+.125*8 = 1... etc.

i'm pretty sure that the most rational person would pay any amount of money to play this game because the weighted mean average of all results is infinity.

e.g. if 1,000,000 people each paid $1000 to play this game, they would probably end up with more money than they started with (as a group)

that is, they would probably have over $1,000*1,000,000 = 1 billion dollars combined at the end of the games.

maybe i'll write a program to test it

[john9blue]

i just thought of a modified version of the problem:

suppose that, for each failed coin toss, you had to split your winnings with someone. for example, if you flipped tails twice, and then flipped heads the third time, you would split your winnings with two other people.

how much money would a rational person pay to play this game, assuming that they are only seeking to maximize their own winnings?

[Haggis_McMutton]

I wouldn't bet on the high stakes one, I don't like high stakes gambles.

I would say 4 dollars would be an enticing number for me to play since I'm not very lucky, Half a chance of losing half the bet, quarter chance of breaking even, quarter chance of winning more. It seems fair enough.

A few questions though
1. Is there any possibility of it being a two headed coin, making me an instant loser?
2. Is there any possibility of it being a two tailed coin, trapping us in some sort of Twilight Zone fate; waiting desperately for the release of death?
3. If so, can I just leave?

Heh, point #2 made me chuckle.
You can inspect the coin to avoid such a fate and leave if you're willing to forfeit the game.

Do we stop the first time it hits heads? In other words, if it hits heads the first time, would I get my $2 and that would be it?

Yeah.

If yes (which I think is the answer), I would try to pay $1.99 but would pay $2. The person running the game would probably want to charge something more than $2, right? My math sucks.

Well, they'd try to charge as much as possible. The question is up to what sum would you be willing to pay.